|
3.热力学第二定律简介及应用 第二定律有多种表达方式,本文使用Boltzmann对熵(entropy)的表述: (24)S=klnΩ (24)中S代表熵,定量一个热力学系统R内部(比如一间屋子)的能量(=热)的分布状况。k是Boltzmann常数,在本文中看做1。Ω可以理解为R中携带能量的分子在给定状态下存在多少种可能的组合方式。用一个常识性的例子来说明(24)的意义:想象一个寒冷的屋子里放进一个烧得通红的铁块。随着时间推移,屋子的整体温度会升高而铁块的温度会下降,直到两者的温度等同。这背后的原理是,携带能量的分子(姑且叫做热分子)在运动中碰撞到不携带能量的分子(冷分子)并把能量传递给后者,而后者又会在运动中碰撞到其他冷分子。这个自然过程表现为热(即能量)在空间的传递,也叫做能量的耗散(energy dissipation)。 能量耗散是一个自然过程,因为热分子的随机运动不可避免,与周边冷分子的碰撞也就不可避免。这个过程还可以从另一个角度来描写。当热铁块刚刚放进冷屋子的时候,能量的分布表现为一种“秩序”或者说“结构”,即有的地方集中的冷,有的地方集中的热。能量耗散的最终结果,是使携带能量的分子随机分布在整个屋子中,从而使原来的系统达到一个新的状态,其无序(chaos)程度上升,即熵值增加。下面看一个量化的例子。 设“屋子”等于一个包含4x5=20个分子的两维空间,“热铁块”是其中的2x2=4个热分子,屋子里的其余16个分子是冷的: 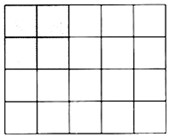 在这个初始状态,我们在屋子里摆放热铁块(即把2x2个热分子作为一个整体来安排)的方式只有12种(4个横移位置乘以三个纵移位置),相当于(24)中的Ω=12,S=ln12=2.485。经过一定时间之后,携带能量的热分子在自然耗散的作用下被随机地分布在整个空间,组合⑥数目Ω=20!/4!(20-4)!=20x19x18x17/4!=4,845,S=ln4,845=8.486。换一个说法,在同一空间中的四个热分子充分耗散会有接近5千种可能的分布,其中碰巧以2x2为一个整体的分布只有12种可能。在自然条件下,后一类情况出现的概率小于全部可能性的1/400,即便我们设定的热力学系统是如此之小。总之,能量的分布从有序向无序转换是“自动”的,在没有其他因素介入的情形下无序(熵值高的)分布的概率远远高于有序(熵值低的)分布。正因如此,暖气片虽然安装在一面墙上却可以温暖整个房间。 (责任编辑:admin) |
