|
3 博弈论模型的求解 在传统的博弈论中,一般都将纳什均衡作为博弈的解。  事实上一个战略组合如果不是纳什均衡,则意味着在这个组合里一定存在某个参与人(当其他参与人选择战略组合给定时),不能使自己的收益最大化。在这种情况下,理性的参与人会偏离该战略,从而使得这个战略组合不能成为博弈的结果。因此,一个战略组合如果不是纳什均衡,就不能成为博弈的解。协调博弈中存在多个纳什均衡点,参与人希望在其中任何一个纳什均衡点上实现各自的最大收益。消歧博弈有两个纯策略纳什均衡{x1,x1},{x2,x2},即双方都选择x1或都选择x2。在这类博弈中,参与人在做选择时,唯一需要关心的就是其他人选择了什么,并据此做出选择。Sen(1967)将一个协调博弈称为“信心博弈”。他指出,协调博弈与囚徒困境博弈刚好相反,每个参与者选择策略A或B,仅仅需要确信对方也会相应地选择A或B。这个博弈的均衡策略中没有明显的优势策略,因此在具体的博弈过程中双方究竟选择哪个均衡还是不确定的。在实际生活中我们可以通过法律规定靠左或靠右行驶,使得交通博弈的某个均衡得以实现。在经济学领域中可以通过契约之类的东西,使得均衡得以实现。 在语言学当中,我们可以通过语法规则实现歧义消除,从而实现博弈论中的某个均衡。但是在我们研究的问题当中,语法规则已经不能进行区分。在这种情况下,两种策略无优劣之分,参与者将其多个纯策略以一定的选取概率进行组合,由此得到的均衡称为混合策略纳什均衡。例如在消歧博弈信息发送者以概率p选择x1,以概率1-p选择x2,信息接收者以概率q选择x1,以概率1-q选择x2。则两人的随机行动((p,1-p),(q,1-q))就是一个混合策略,当它满足纳什均衡条件时就是一个混合策略纳什均衡。这乍看起来似乎不可思议,实际上冯志伟(1985)已指出在人们用语言进行交际活动时,语言成分的使用会出现随机性,因此,可以使用统计的方法对其进行研究;语言统计、数理统计以及信息论等数学工具都可以用来研究语言成分出现的概率和频率,从而揭示语言的统计规律。 下面我们从信息接收者的角度分析“{牛奶咖啡}”这个歧义问题的混合策略纳什均衡。假设发送者选择x1的概率为p,则选择x2的概率为1-p。在实际应用中,接收者如何得到发送者选择某一意思的概率,一般可以从语料库中统计出每种意思出现的频率,用这个频率近似概率,作为这里的p。如果x1={牛奶咖啡}(定中结构,牛奶口味的咖啡)出现的概率为p,则x2={牛奶咖啡}(并列结构,牛奶和咖啡)出现的概率就是1-p。因此,接收者已知发送者的选择概率的假设是合理的,在此情况下接收者采取什么样的策略才能使自己的收益最大化呢?因为发送者不会始终重复地选择某个策略,这种情况下接收者不可能有合适的纯策略,他必须在两个策略之间随机选择。他以一定的概率来选择每个意思,使得自己的收益达到某种意义下的最优。接收者在该条件下选择x1和x2的期望收益分别为: 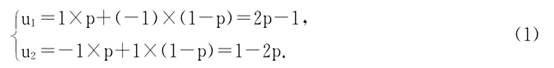 显然,接收者使自己收益最大化的一个基本选择是,当u1>u2,即p>1/2时,接收者选择x1,否则选择x2。 根据上面的选择策略,等价于选择出现概率大的那个意思,那么这个策略和传统的基于统计的歧义消除方法相同。博弈论的理论方法表明,在没有其他相关信息的条件下,基于概率的选择方法不失为一种好方法。我们将这种方法称为最大概率法,该方法的一个重要缺陷是在求解过程中使用频率较低的意思始终不会被选择,因此当发送者发送频率低的意思时总不能得到正确的理解,并且在重复多次的使用中得到同样的结果,错误永远不能得到纠正。当选择者以概率q和1-q选择x1和x2时,他的期望收益为qu1+(1-q)u2。我们希望选择一个,在发送者以不同的概率发送x1和x2时,接收者的期望收益始终非负。当接收者以与发送者相同的概率选择意思时,即令q=p,此时期望收益变为p的函数: (责任编辑:admin) |
