|
由此得到这样的抽吸引理:设 L是一个正则语言,那么,必定存在着符号串x,y和z,使得对于n≥0,有y≠Ø(空符号),并且xynz∈ L｡ 抽吸引理告诉我们,如果一种语言是正则语言,那么,就可以找到一个符号串y,这个y可以被抽吸｡ 前面说过,语言{anbn}不能由正则语法生成;现在,用抽吸引理来证明语言{anbn}不是正则语言｡为此必须证明,我们取的任何符号串s都不可能被分成x,y和z三个部分,使得y能够被抽吸｡随意给一个由{anbn}构成的符号串s,我们可以用三种办法来分割s,并且证明,不论用哪一种办法,都不可能找到某个y能够被抽吸｡  由此可见,在语言{anbn}中没有符号串能够被分割为x,y,z,使得y能够被抽吸,所以,{anbn}不是正则语言｡ 为了满足自然语言计算复杂性的要求,Chomsky(1959)主张采用上下文无关语法来描述自然语言｡上下文无关语法的重写规则的形式是 A→ω,其中,A是单独的非终极符号,ω 是异于Ø的符号串,即|A|=1≥|ω|｡ 尽管{anbn}不是正则语言,不过{anbn}是上下文无关语言,下面就提出上下文无关文法来生成{anbn}: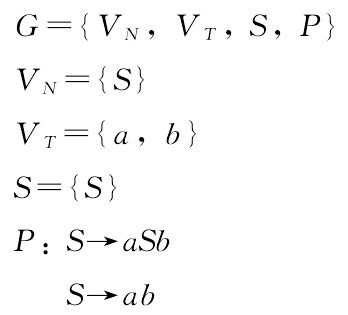 
(责任编辑：admin) |