|
一 关于自然语言的计算复杂性(computational complexity)的研究是语言学理论中一个重要而饶有趣味的问题,许国璋先生敏锐地关注到这个问题,说明了他的远见卓识。 Chomsky(1956,1957,1959,1963)建立了形式语言理论(formal language theory)的完整系统,首先关注到自然语言的计算复杂性。在形式语言理论中,Chomsky提出了不同于传统语法的形式语法(formal grammar)的定义,把形式语法理解为有限规则的集合,这些规则可以生成语言中的合格句子,并排除语言中的不合格句子。 形式语法的符号用G表示,语法G所生成的形式语言用L(G)表示。形式语言是一种外延极为广泛的语言,它既可以指自然语言,也可以指各种用符号构成的语言(例如,计算机使用的程序设计语言)。Chomsky把自然语言和各种符号语言放在一个统一的平面上进行研究。 Chomsky把形式语法G定义为四元组: 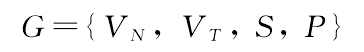 其中,VN是非终极符号,不能处于生成过程的终点,VT是终极符号,只能处于生成过程的终点;VN与VT不相交,没有公共元素;S是VN中的初始符号;P是重写规则,其一般形式为:φ→ψ,其中的 φ和ψ都是符号串。 如果用符号#来表示符号串的界限,那么,可从初始符号串#S#开始,应用重写规则#S#→#φ1#,从#S#构成新的符号串#φ1#,再利用重写规则#φ1#→#φ2#,从#φ1#构成新的符号串#φ2#,……,一直到得出不能再继续重写的符号串#φn#为止,这样得出的终极符号串#φn#,就是形式语言L(G)中合格的句子。 Chomsky根据重写规则的形式,把形式语法分为4类。 对于形式语法G={VN,VT,S,P},其重写规则为φ→ψ,并且要求φ≠Ø。为了给语法进行分类,Chomsky对其重写规则加上一些限制:  (责任编辑:admin)
(责任编辑:admin) |
