|
限制1要求语法的重写规则全都具有形式φ1Aφ2→φ1ωφ2,这样的重写规则在上下文φ1-φ2中给出A→ω。显然,在这种情况下,ψ这个符号串的长度(即ψ中的符号数)至少等于或者大于φ这个符号串的长度(即φ中的符号数),如果用|ψ|和|φ|分别表示符号串ψ和φ的长度,则有|ψ|≥|φ|。由于在重写规则φ1Aφ2→φ1ωφ2中,每当A出现于上下文φ1-φ2中的时候,可以用ω来替换A,因此,把加上了限制1的语法叫做上下文有关语法(context-sensitivegrammar)或1型语法(type 1grammar)。 限制2要求语法的重写规则全都具有形式A→ω,这时上下文φ1-φ2是空的,在运用重写规则时不依赖于单个的非终极符号A所出现的上下文,因此,把加上了限制2的语法叫做上下文无关语法(context-free grammar)或2型语法(type 2grammar)。 限制3要求语法的重写规则全都具有形式A→aQ或者A→a,其中,A和Q是非终极符号,a是终极符号,这种语法叫做正则语法(regular grammar)或3型语法(type 3grammar),又叫做有限状态语法(finite state grammar)。 没有上述限制的语法,叫做递归可枚举语法(recursive enumerable grammar)或0型语法(type 0 grammar)。 显而易见,每一个正则语法都是上下文无关的,每一个上下文无关语法都是上下文有关的,每一个上下文有关语法都是0型的。这样,我们可把由0型语法生成的语言叫0型语言(type 0 language),把由上下文有关语法、上下文无关语法、正则语法生成的语言分别叫做上下文有关语言、上下文无关语言、正则语言,也可分别叫做1型语言(type 1 language)、2型语言(type 2language)、3型语言(type 3language)。由于从限制1到限制3的限制条件是逐渐增加的,因此,不论对于语法或对于语言来说,都有 任何的正则语法(3型语法)一定包含在上下文无关语法(2型语法)、上下文有关语法(1型语法)、递归可枚举语法(0型语法)中,任何的上下文无关语法(2型语法)一定包含在上下文有关语法(1型语法)、递归可枚举语法(0型语法)中,任何的上下文有关语法(1型语法)一定包含在递归可枚举语法(0型语法)中,这就是语法的 Chomsky层级(Chomsky hierarchy),如图1所示。 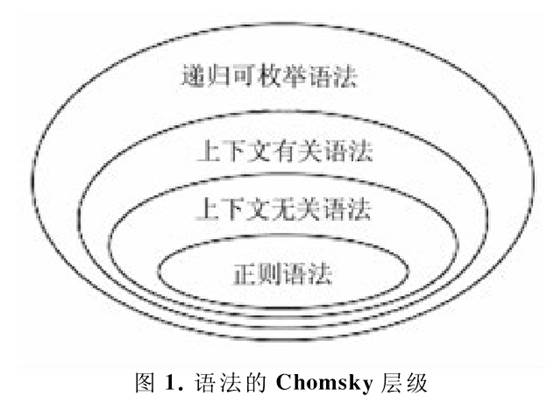 Chomsky认为,根据这样的形式语言理论,可以采用有限的规则来描述形式上是潜在地无限的句子,从而达到以简驭繁的目的。 (责任编辑:admin) |
