|
一、引言 《红楼梦》这部小说对于中国人来讲是非常特殊的,它自问世以来,脍炙人口两百余年,至今不衰。19世纪后半叶,在北京流行的《京师竹枝词》中竟有“开谈不说红楼梦,纵读诗书也枉然”之言,其受人爱好可以想见。然而曹雪芹在给后人留下《红楼梦》这部伟大作品的同时,也给人们留下了很多的谜团,“寿怡红群芳开夜宴”(第六十三回)中群芳的座次问题就是其中的一个。由于第六十三回在整部《红楼梦》中具有特殊地位,所以“怡红夜宴图”的原貌究竟如何引起了很多人的兴趣,著名红学家俞平伯先生、周绍良先生、邓云乡先生以及彭昆仑先生都曾讨论过这一问题[1][2]。本文从一个新的角度,应用数学中线性方程组的知识来讨论这一有趣的问题。 二、问题的提出 为方便讨论,先将《红楼梦》第六十三回中的相关原文摘录于下[3]: (一)说着,晴雯拿了一个竹雕的签筒来,里面装着象牙花名签子,摇了一摇,放在当中。又取过骰子来,盛在盒内,摇了一摇,揭开一看,里面是五点,数至宝钗。 (二)宝钗又掷了一个十六点,数到探春,探春笑道:“我还不知得个什么呢。” (三)探春哪里肯饮,却被史湘云、香菱、李纨等三四个人强死强活灌了几口下去。探春只命蠲了这个,再行别的,众人断不肯依。湘云拿着她的手,强掷了个十九点出来,便该李氏掣。 (四)李氏摇了一摇,掣出一根来一看,笑道:“好极。你们瞧瞧,这劳什子竟有些意思。”众人瞧那签上,画着一枝老梅,是写着“霜晓寒姿”四字,那一面旧诗是:竹篱茅舍自甘心。注云:“自饮一杯,下家掷骰。”李纨笑道:“真有趣,你们掷去罢。我只自吃一杯,不问你们的废与兴。”说着,便吃酒,将骰过与黛玉。 (五)黛玉一掷,是个十八点,便该湘云掣。湘云笑着,揎拳掳袖的伸手掣了一根出来。大家看时,一面画着一枝海棠,题着“香梦沉酣”四字,那面诗道是:只恐夜深花睡去。黛玉笑道:“‘夜深’两个字,改‘石凉’两个字。”众人便知她趣白日间湘云醉卧的事,都笑了。湘云笑指那自行船与黛玉看,又说:“快坐上那船家去罢,别多话了。”众人都笑了。因看注云:“既云‘香梦沉酣’,掣此签者不便饮酒,只令上下二家各饮一杯。”湘云拍手笑道:“阿弥陀佛,真真好签!”恰好黛玉是上家,宝玉是下家。 (六)湘云便绰起骰子来,一掷个九点,数去该麝月。麝月便掣了一根出来。大家看时,这面上一枝…… (七)麝月一掷个十九点,该香菱。香菱便掣了一根并蒂花,题着“联春绕瑞”,那面写着一句诗…… (八)香菱便又掷了个六点,该黛玉掣。黛玉默默的想道:“不知还有什么好的被我掣着方好。” (九)黛玉也自笑了。于是饮了酒,便掷了个二十点,该着袭人。袭人便伸手取了一支出来…… (十)宝玉忙说:“林妹妹怕冷,过这边靠板壁坐。”又拿个靠背垫着些。袭人等都端了椅子,在炕沿下一陪。 (十一)二人斟了两杯,只得要饮。宝玉先饮了半杯,瞅人不见,递与芳官,端起来便一扬脖喝了。黛玉只管和人说话,将酒全折在漱盂内了。 从上述几段文字中,我们可以看到,在为宝玉庆祝生日的“怡红夜宴”中,众人正在玩掷骰子抽签的游戏:首先由晴雯开局,她摇出的骰子点数是五点,数至宝钗,由宝钗抽签;宝钗抽完签后,由宝钗掷骰子,掷出的骰子点数是十六点,数到探春,由探春抽签;探春抽完签后,再由探春掷骰子决定下一个抽签者……依此类推,最后由袭人收局,游戏结束。由此我们可以提出一个问题:在“怡红夜宴”中,怡红群芳究竟是按怎样的座位次序来就座的?能否给出一个“怡红夜宴图”来反映当时的情景?弄清楚这一问题,对于理解书中内容是很有帮助的。下面我们通过建立数学模型的方法来解决这一问题。 三、数学模型的建立及求解 从《红楼梦》的描写当中我们知道,参加这次夜宴的总共有16人,即:晴雯、宝钗、探春、李纨、黛玉、湘云、宝玉、麝月、香菱、袭人、芳官、宝琴、碧痕、四儿、春燕、秋纹。其中前面10人在夜宴的掷骰子抽签游戏中被提及到(参见上面的引文(一)~(九)),从描写的场景中我们可以知道各人所掷出的骰子点数;后面的6人没有在游戏中讲到,这给问题的解决带来了困扰,但只要能够先确定出前面10人的座位情况,则问题的解决就相对容易了。因此现在问题的关键,是根据各人所掷出的骰子点数先来确定出前面10人的座位号,这可以通过解线性方程组来加以解决。 我们首先作如下两个假定:①在游戏进行中,按掷出的骰子点数来数人时,从掷骰者本人数起(注:也可假定从掷骰者下家数起,这样会得到另外的结果,但这并不是本质的);②按掷出的骰子点数来数人时,是按逆时针方向来数(注:也可假定是按顺时针方向来数,这样会得到另外的结果,但这同样不是本质的) 设前面10人的座位号分别用如下的整型变量来表示:X1:晴雯;X2:宝钗;X3:探春;X4:李纨;X5:黛玉;X6:湘云;X7:宝玉;X8:麝月;X9:香菱;X10:袭人。又设xi*(i=1,2,…,10)表示各人座位号与骰子点数之和,则xi与xi*(i=1,2,…,10)之间的关系为: 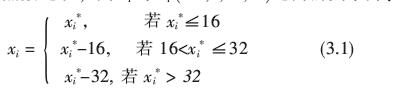 易知xi*的值不会超过40,因为座位号的最大值是16,而骰子点数的最大值是24,所以必有xi*荞40,因此(3.1)式已经完全反映了xi与xi*之间的关系(注:这里是按每次掷4颗骰子来计算,若按每次掷5颗骰子来计算,则骰子点数的最大值是30,故必有xi*荞46,此时(3.1)式也完全反映了xi与xi*之间的关系,所以并不影响后面的计算。在《红楼梦》中并没有点明是掷4颗骰子还是掷5颗骰子,应该说两者皆有可能,不过由以上分析可知,对于我们所考虑的座次问题而言,这一点并没有造成什么影响)。 现在,在上面所作的两个假定下,根据引文(一)~(九)的描写,我们可得如下的线性方程组: 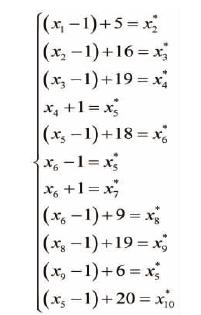 令x1=1,代入方程组(3.2),再利用(3.1)式即可逐步解出各xi*(i=1,2,…,10)之值。求解的结果如下:X1=1(晴雯),X2=5(宝钗),X3=4(探春),X4=6(李纨),X5=7(黛玉),X6=8(湘云),X7=9(宝玉),X8=16(麝月),X9=2(香菱),X10=10(袭人)。根据这些结果,就可以排出“怡红夜宴”中各人的座位情况了。 四、怡红夜宴图 根据上面的求解结果,我们可以先排出晴雯、宝钗等10人的座位,然后再确定剩余6人的座位,我们所排出的“怡红夜宴图”如下图所示: 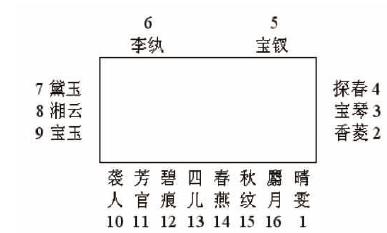 对上述示意图我们作如下说明:①在示意图中,晴雯、香菱、探春、宝钗、李纨、黛玉、湘云、宝玉、袭人、麝月这10个人的座位是由上面求出的解所决定的;②由引文(十一)可知,芳官的座位离宝玉较近,故将芳官的座位排在袭人之旁(即座位11)较为合理;③宝琴在书中描写的游戏中没有提及到,但由于其身份,必坐于炕沿之上,而炕沿上已有7个座位(炕沿上总共应有8个座位)固定,所以宝琴事实上只能坐在香菱与探春之间的这一个座位(即座位3)上了;④碧痕、四儿、春燕、秋纹这四人在书中描写的游戏中也没有提及到,但前面已经确定了12个人的座位,所以这四人只能坐在剩余的四个座位上(即:座位12、13、14、15),至于她们四人之间,由于信息不足,其座位次序还不能完全固定,四人之间可以随意交换(上面示意图中给出的只是其中的一种);⑤由引文(十)可以进一步印证上面示意图中的座位排法是合理的。 五、结语 《红楼梦》第六十三回是作者浓墨重写和精心设计的部分,“在八十回内为太虚幻境以后最重要的全书人物的提纲,而为群芳与宝玉关系及其身世之总结”[1]。因此本回书因包含了很多理解全书内容的重要信息而为历来的红学研究者所关注,弄清楚“怡红夜宴”中群芳的具体座次方位也就引起很多人的兴趣,它对于理解书中一些内容的含义是有帮助的,正像俞平伯先生所言,“图出于书,图方可信,以书合图,书乃更明”[1]。我们从《红楼梦》的几段原文出发,通过建立线性方程组模型的方法来得出“怡红夜宴图”,还原了《红楼梦》中的夜宴场景,方法简单而结果合理,故记于此,以供世之好谈“红学”者参考。 参考文献: [1]俞平伯.红楼梦研究[M].上海:复旦大学出版社,2004:213~229. [2]彭昆仑.还“怡红夜宴图”的本来面目[J].红楼梦学刊,1986(3):215~234. [3]曹雪芹.红楼梦(蔡义江增评校注本)[M].北京:作家出版社,2007:771~789. 原载:《德宏师范高等专科学校学报》2011年第3期 原载:《德宏师范高等专科学校学报》2011年第3期 (责任编辑:admin) |
