|
4 试验结果 我们将上节给出的三种方法编写程序,对从实际语料中选取出的100条包含“n+n”歧义的语料进行处理,检验它们的效果。首先我们对这些语料进行了分词和词性标注等处理。然后,对每一个“n+n”歧义结构,统计其两种不同意思的使用频率p和1-p,根据图1的博弈矩阵建立博弈论模型。最后分别使用最大概率法、基本博弈论方法和包含上下文信息的博弈论方法对这些歧义结构混在句中进行分析处理。 我们使用三种方法对语料进行消歧,并统计每次错误数占总数的百分比。对于博弈方法由于消歧结果都是基于概率,在一次具体的使用过程中,只有对错两种具体的结果。只有对大量问题或者同一问题的反复求解中才能体现出以较大的概率选择正确结果的效果。受语料规模所限,我们用三个算法分别对这100条语料消歧,对每条语料执行10次,计算其错误百分比来得到错误率。这样也可以模拟算法对1000条语料消歧的效果。图3是每种方法的消歧情况。横坐标表示语料,纵坐标是错误百分比。 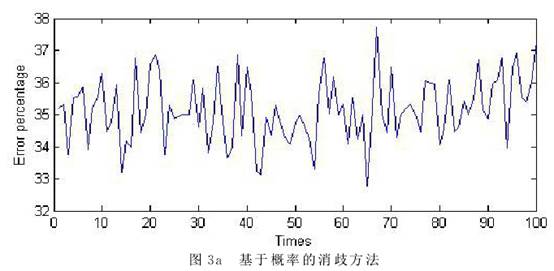 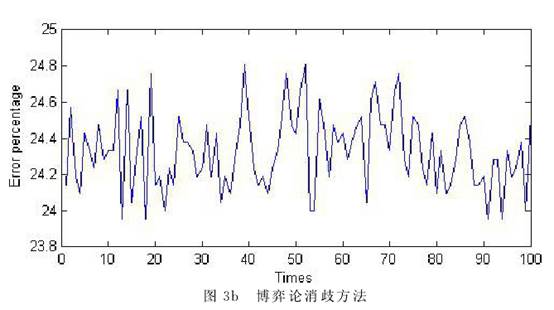 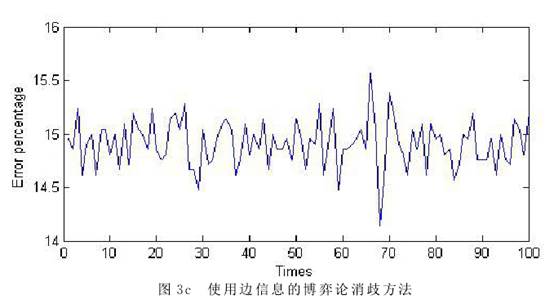 从图3可以看出,仅使用频率进行消歧,最大错误率在35%左右(图3a),因为10次的执行结果都相同。采取基本博弈论方法进行消歧,10次的结果各不相同,在重复的执行中有机会修正错误,因此最大错误率减少了10%左右,均小于25%(图3b)。当使用基于上下文信息的博弈论方法时,由于有了更多的信息,因此最大错误率进一步减少,达到15%左右(图3c)。 要对更加精确的模型和相应算法展开大规模和深入的实验验证,首先要有大规模的语料进行支撑。其次要对这些语料进行必要的前期处理,对不同的歧义结构出现的频率、伴随信息的数量、特征及权重等都需要进行标注。受到现实条件的限制,本文仅对语料库中出现的100条“n+n”结构的歧义现象建立博弈论模型,采取三种方法进行了消歧实验,结果证明使用博弈论的思想和方法处理结构歧义问题是行之有效的。 (责任编辑:admin) |
